Vega Options Explained: Price Sensitivity to Volatility

In the world of options trading, understanding the impact of price and volatility on the value of your contracts is crucial. One key component in evaluating these factors is Vega, the options trading Greek. It measures an option's sensitivity to changes in implied volatility. This article will explore Vega meaning in options.

Key Takeaways

• Vega measures an option's price sensitivity to changes in implied volatility.
• Vega plays a critical role in options pricing and risk management.
• Understanding Vega can help traders make more informed decisions in the cryptocurrency options market.

The Options: Greek Vega Explained

Vega (volatility sensitivity) is an essential aspect of derivatives trading, as it allows traders to understand and manage the potential impact of changes in implied volatility (IV) on their options positions. Vega is often designated by the Greek letter 𝓥 (nu).

What Is Vega In Options Trading?

Let’s start with the vega definition in regard to options trading. Vega is one of the "Greeks" used in options trading to assess the risk and potential rewards associated with a particular option. Specifically, Vega measures the change in the option’s value with respect to the implied volatility in the underlying asset's price. A higher Vega indicates that the option's price is more sensitive to changes in implied volatility, while a lower 𝓥 implies less sensitivity.

Options Vega Math

Vega is calculated as the first derivative of an option's price with respect to changes in implied volatility. In other words, it shows the expected change in the option's price for a one percentage point increase in implied volatility. Vega is typically expressed in dollars per one percentage point change.

Implied Volatility

Implied volatility (IV) is a measure of the market's expectation of future price fluctuations for a base crypto asset, such as Bitcoin. As implied volatility increases, the price of options tends to rise, and vice versa. This relationship is captured by Vega, which quantifies how sensitive an option's price is to changes in IV.

Strike and Spot Price

The strike price (exercise price) of an option is the predetermined price at which the owner can buy (call option) or sell (put option) the base asset. The spot price refers to the current market price of the asset. The distinction between the exercise price and the spot price influences the value of an option and its Vega.

How Vega Changes

Vega is not constant and can change due to various factors. Let's explore these factors in more detail.

Vega and Time to Expiration

As an option's time to expiration decreases, the Vega tends to decrease for options that are at-the-money or near-the-money. Conversely, the 𝓥 of deep in-the-money or far out-of-the-money options may increase as time to expiration approaches.

Vega and Volatility

Vega is positively correlated with implied volatility. When IV increases, Vega also increases, indicating that the option's price is more sensitive to changes in volatility.

Vega and Strike Price

Vega can vary depending on the strike price. Options with exercise prices further away from the current market price (out-of-the-money) typically have higher 𝓥 values than those with exercise prices closer to the market price (at-the-money or in-the-money).

Positive and Negative Vega

Vega can be either positive or negative, depending on whether the trader holds a long or short position in the option.

In a long position, the trader has purchased the option and stands to profit from an increase in IV, resulting in a positive volatility sensitivity.

In a short position, the trader has sold the option and would benefit from a decrease in IV, resulting in a negative Vega.

Long and Short Vega Positions

Traders can establish long Vega positions by purchasing options or constructing complex strategies, such as straddles or strangles. These positions benefit from increasing implied volatility.

Short 𝓥 positions, on the other hand, involve selling options or employing strategies like covered calls, which profit from decreasing IV.

Vega and Bid-Ask Spread

The bid-ask spread is the distinction between the highest price a buyer is willing to pay (bid) for an asset and the lowest price a seller is willing to accept (ask). In options trading, the bid-ask spread can be impacted by Vega, as changes in anticipated volatility can affect the contract's price, leading to changes in the bid and ask prices.

Calculating Options Prices with Vega

There are various methods to calculate options prices, including the Black-Scholes Model and Excel VBA. Vega plays an essential role in these calculations, helping traders assess the impact of implied volatility on their options positions.

Black-Scholes Model

The Black-Scholes Model is a widely-used formula for pricing European-style options. It takes into account several variables, including the underlying asset's price, the option's strike price, time to expiration, risk-free interest rate, and implied volatility. Vega is one of the outputs of the model, providing valuable information on the option's sensitivity to changes in IV.

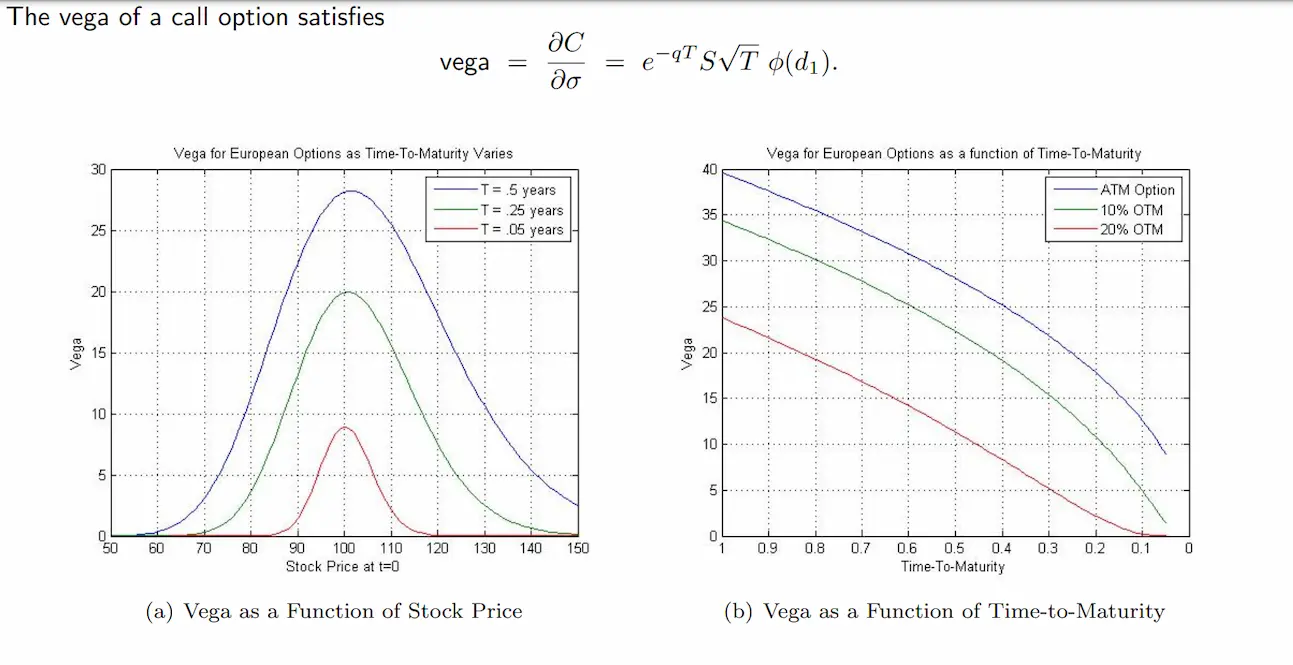
Excel VBA

Visual Basic for Applications (VBA) is a programming language built into Excel application. It can be used to create custom functions for calculating options prices, including Vega. By incorporating 𝓥 into their calculations, traders can gain a better understanding of how implied volatility affects their options positions and make more informed decisions.

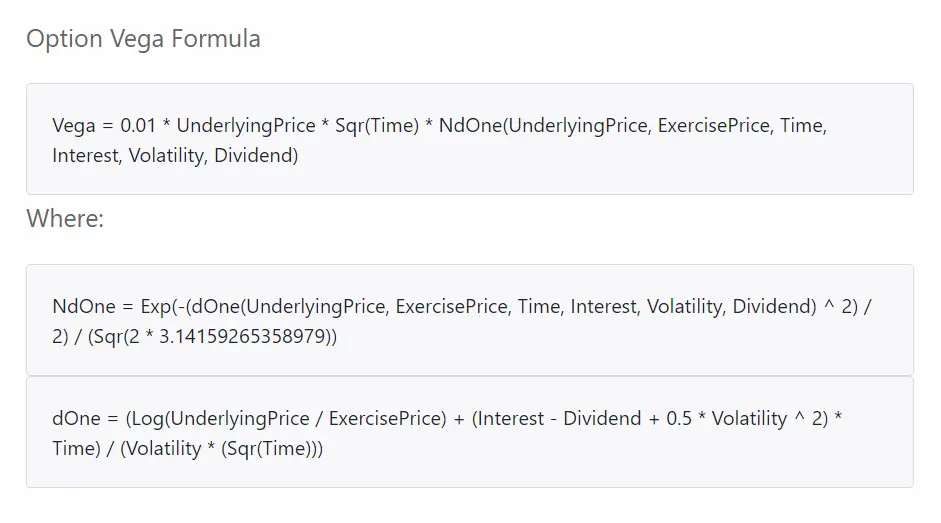
How to Use Vega

Vega can be used in various ways to inform trading decisions, manage risk, and optimize options portfolios. One common application is through the analysis of an option's Vega chain.

Vega Options Chain

An option chain is a table displaying the prices, volume, and other information for options on a specific base asset. A Vega option chain shows the Vega values for each option on the chain, allowing traders to identify options with higher or lower sensitivity to changes in IV. By analyzing the 𝓥 chain, traders can assess potential risks and opportunities in their options strategies.

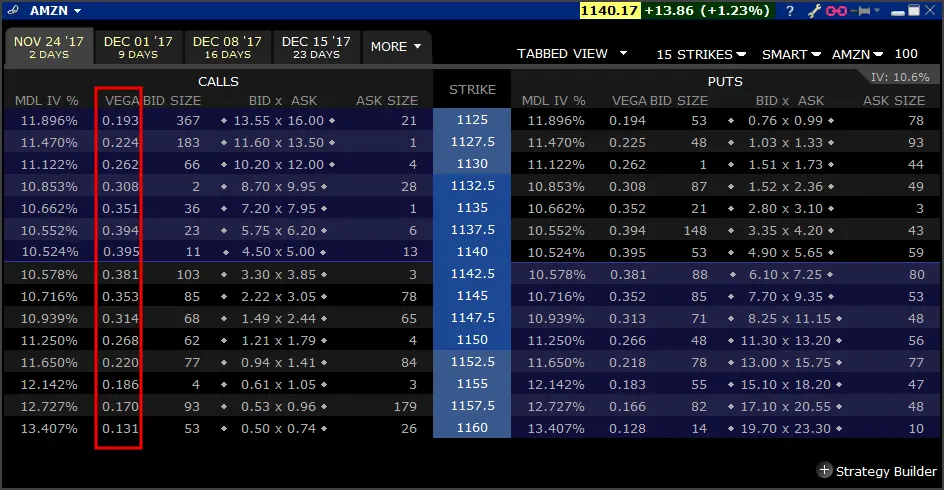
Example of Vega

Let's consider a simple example of Vega using Bitcoin options. Suppose that Bitcoin is currently trading at $20,000, and a trader is considering purchasing a call option with a strike price of $21,000 and an expiration date one month away. The option has a Vega value of 0.25.

If IV increases by 1%, the option's price would be expected to increase by 0.25 * 1% = 0.0025, or 0.25% (assuming other factors remain constant).

Conversely, if IV decreases by 1%, the derivative contract's price would be expected to decrease by 0.25 * 1% = 0.0025, or 0.25%.

Which Options Have the Most Vega?

Options with longer time to expiration and strike prices further away from the current market price (out-of-the-money) generally have higher Vega values. This means they are more sensitive to changes in implied volatility, offering greater potential rewards but also higher risk.

Implications of Put-Call Parity on Vega

Put-call parity is a fundamental principle in options pricing that establishes a relationship between the prices of European-style call and put options with the same exercise price and time to expiration.

In the context of Vega, put-call parity implies that the 𝓥 values for corresponding call and put options are equal. This relationship can help traders identify arbitrage opportunities and maintain balanced portfolios.

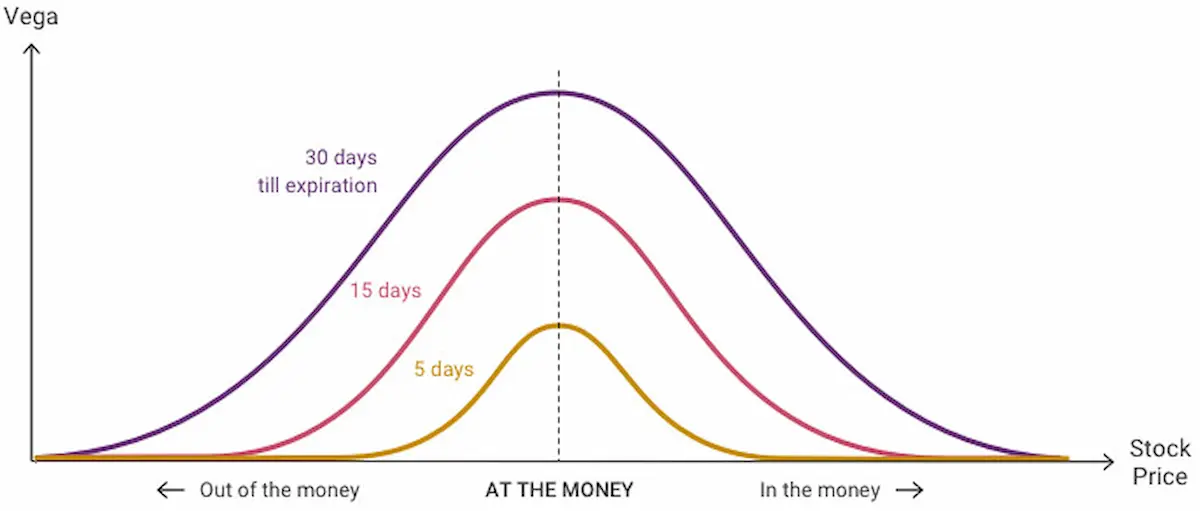
Vega Graphs - When Is Vega Highest?

Vega tends to be highest for at-the-money (ATM) options with longer time to expiration. As the option moves further in-the-money (ITM) or out-of-the-money (OTM), the Vega generally decreases. Additionally, as time to expiration shortens, Vega tends to decrease for at-the-money and near-the-money options. By analyzing 𝓥 graphs, traders can identify the optimal strike prices and expiration dates for their options strategies.

Conclusion

Understanding Vega in options trading is essential for managing risk and optimizing returns. By analyzing the sensitivity of options prices to changes in implied volatility, traders can make more informed decisions and better navigate the complex world of cryptocurrency options.

FAQs

1. What Does Vega Mean In Options

Vega represents the degree to which an option's theoretical value fluctuates in response to shifts in implied volatility. It can be described as the amount of theoretical value gained or lost when there is a 1-percent increase or decrease in implied volatility. For example, consider an option with a Vega of 0.25 and an underlying asset value of $10. Should the volatility experience a 1% uptick, the option's worth would subsequently rise to $10.25.

2. How Does Vega Affect Option Price When Implied Volatility Changes?

Vega measures the sensitivity of an option's price to changes in implied volatility. A higher Vega indicates that the option's price is more sensitive to changes in IV, while a lower 𝓥 implies less sensitivity. When implied volatility increases, the price of an option with positive Vega will rise, and when IV decreases, the option's price will fall.

3. How Does Vega Differ Between Call and Put Options?

Due to put-call parity, the Vega values for corresponding call and put options with the same exercise price and time to expiration are equal. Both call and put options will have positive 𝓥, meaning their prices will increase with rising implied volatility and decrease with falling IV.

4. How Does Time to Expiration Affect Vega?

Time to expiration affects Vega differently for various types of options. For at-the-money and near-the-money options, Vega tends to decrease as time to expiration shortens. However, for deep in-the-money and far out-of-the-money options, Vega may increase as time to expiration approaches.

5. How Can Traders Use Vega in Their Options Trading Strategies?

Traders can use Vega to assess the risk and potential rewards associated with their options positions, manage their exposure to changes in implied volatility, and identify opportunities in the options market. By analyzing 𝓥 option chains, traders can choose contracts with higher or lower sensitivity to changes in IV, depending on their risk tolerance and market outlook. Additionally, understanding the relationship between Vega and other factors, such as time to expiration and exercise price, can help traders optimize their options strategies.

*This communication is intended as strictly informational, and nothing herein constitutes an offer or a recommendation to buy, sell, or retain any specific product, security or investment, or to utilise or refrain from utilising any particular service. The use of the products and services referred to herein may be subject to certain limitations in specific jurisdictions. This communication does not constitute and shall under no circumstances be deemed to constitute investment advice. This communication is not intended to constitute a public offering of securities within the meaning of any applicable legislation.