Delta Options: Definition, Calculation, Trading
Key Takeaways:
- Delta, a member of the option Greeks family, measures the relationship between an option's value fluctuations and corresponding movements in the price of the underlying asset.
- The range of deltas extends from 0 to 1/-1 depending on the trade’s side and direction.
- Both short and long traders can use delta in their strategies.
- Delta can be used for identifying directional bias, hedge ratio and probability ratio calculations.
What is Delta in Options Trading?
The value of crypto options contracts is impacted by several factors, including the current market value of the underlying cryptocurrency, the duration until expiration and implied volatility, among others. And to measure the sensitivity of the contract price to changes in these factors, so-called Greeks (delta, gamma, theta, vega, rho) are used. Each of these metrics measures the sensitivity of the option price to particular factor changes. Thus, one of the most important metrics is Delta.
Delta represents the degree to which an option's value reacts to shifts in the underlying asset’s value. It essentially indicates the magnitude of an option’s price change in response to a one-dollar movement in the underlying instrument’s value. The delta for call options varies from 0 to 1, while for put options, it ranges from -1 to 0.
A delta of 1/-1 for call/put options suggests that the option’s price movement aligns with that of the underlying asset. By contrast, a delta of 0 implies that the option’s price is completely unresponsive to fluctuations in the underlying asset’s value.
Definition and Examples of Delta Strategy in Crypto Options Trading
However, delta by itself has no much practical value without its application as part of certain trading strategies, such as delta strategies. A delta strategy involves using option delta to create a trending or neutral trading position in relation to the direction of the asset. Thus, a delta strategy is essentially for buying or selling options based on their delta.
There are many strategies in cryptocurrency options trading that use delta. Here are a few of them:
- Delta-Directional Strategy is a strategy that is used to make money on the estimated direction of the price of the underlying cryptocurrency by buying or selling options with a high delta. For example, if a trader expects the value of a cryptocurrency to rise, he or she might buy high-delta call options to make money on the price change.
- Delta Scaling is a strategy that relies on buying or selling options with different deltas in order to change the size of the position depending on changes in the price of the underlying cryptocurrency. For example, if the value of the crypto asset increases, then the trader can increase the position in сall options contracts with a higher delta to earn more profit.
- Delta-Time Strategy is a strategy that is used to capitalize on changes in the time to expiration of an option. The trader buys options with a longer expiration time and high delta and sells options with a shorter expiration time and low delta. For example, a trader might buy call options with a delta greater than 0.7 and a one-year expiration. Then, they can sell call options with a delta less than 0.3 and a one-month expiration to earn on the difference in the price of the options.
As with any trading strategy, traders must consider the potential risks of each strategy. In addition, traders can use other Greeks, such as gamma and theta, to create a solid trading strategy.
Alternatives to Delta
While delta serves as a valuable indicator of an option contract's sensitivity to fluctuations in the underlying cryptocurrency’s price, yet it is not the exclusive metric that meets the purpose. Other metrics like gamma, vega, and theta also play a role.

Gamma reflects the rate of change in the delta as the value of the underlying instrument moves. It reaches its highest value for in-the-money options and declines as the option becomes more out of the money.
Vega measures the sensitivity of the option to changes in implied volatility, denoting how much the option's price would alter in response to variations in market volatility levels.
Theta reflects the pace at which an option's value declines as it approaches its expiration date. This metric is at its zenith for in-the-money options and decreases as the option moves further out of the money.
What It Means for Individual Investors
Understanding delta enables traders to control risks by adjusting positions in response to the changes in the underlying cryptocurrency’s value, volatility, and the remaining time until expiration.
In addition, delta can be used in combination with other Greeks, such as gamma and theta, to create more complex strategies, such as “straddle” and “strangle”. Such strategies allow one to guard against potential losses or earn on changes in the value of the underlying instrument.
How To Get Delta
Delta can be calculated using various option pricing models, such as the Black-Scholes model or the binomial model. However, most cryptocurrency exchanges automatically provide delta values for option contracts, so traders do not need to calculate them manually. Still, traders are better to understand how deltas are calculated and how they are affected by changes in the underlying digital asset price, volatility, and time to expiration.
Understanding Delta Values
Delta values can range from 0 to -1 and from 0 to 1 for put and call options, respectively. The magnitude of the delta indicates the option's sensitivity to changes in the underlying cryptocurrency’s price, while the sign indicates whether the option is a call or put option.
The question may arise, what is a good delta for options? Essentially, the “good” delta depends on your trading goals, investment timeframe, and appetite for risk. Below, there is a general description of delta values which may serve as guidelines for you.
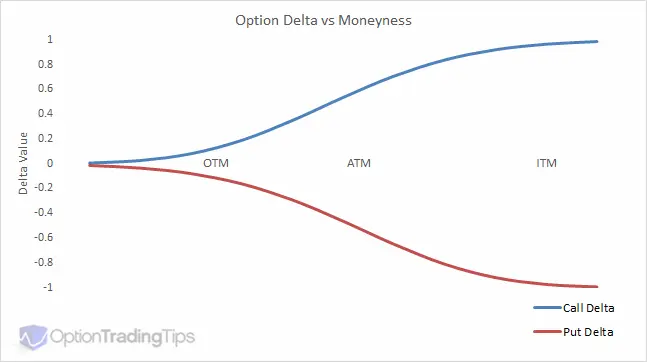
What Delta Measures
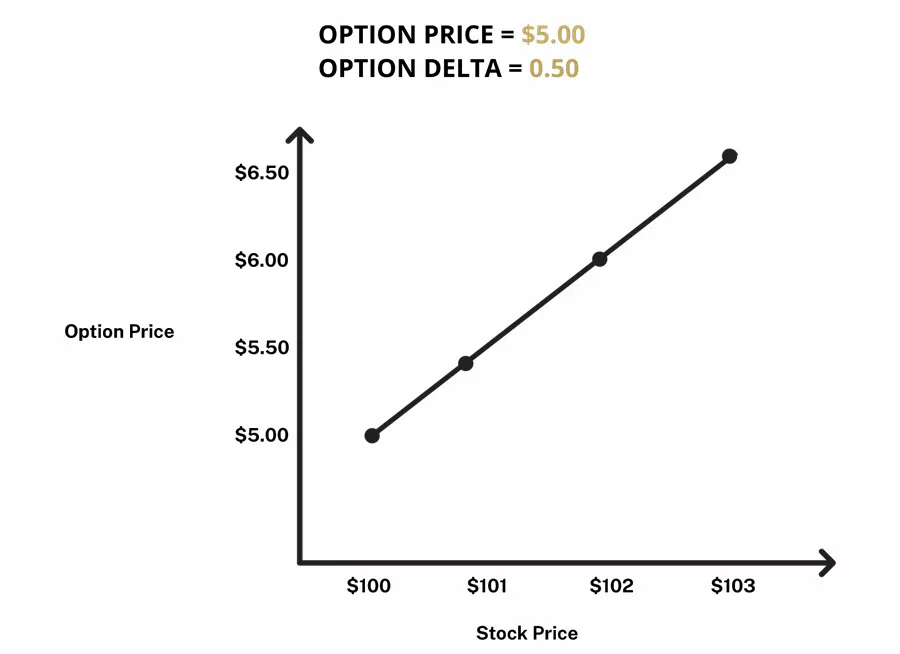
Delta quantifies the change in an option’s value in response to fluctuations in the underlying asset's price. With a delta of 0.5, a $1 shift in the underlying cryptocurrency’s price corresponds to a 50-cent change in the option's value. Conversely, a delta of 1 signifies that each $1 cryptocurrency price movement leads to an equivalent $1 alteration in the option's value.
Deltas for Call Options
Calls are assigned a positive delta, which is explained by the fact that call option prices are positively correlated with the underlying cryptocurrency price. The delta of a call option can range between 0 (0 percent) and 1 (100 percent).
The meaning of delta equal to 1 for call options is that the option is deeply in-the-money and will move in lockstep with the underlying cryptocurrency’s price. A delta of 0.5 means that the call option is at-the-money and has a 50% chance of expiring in-the-money.
Deltas for Put Options
Puts are assigned a negative delta, because put option prices are negatively correlated with the underlying cryptocurrency value. Delta values of a put option can range between 0 (0 percent) and 1 (100 percent).
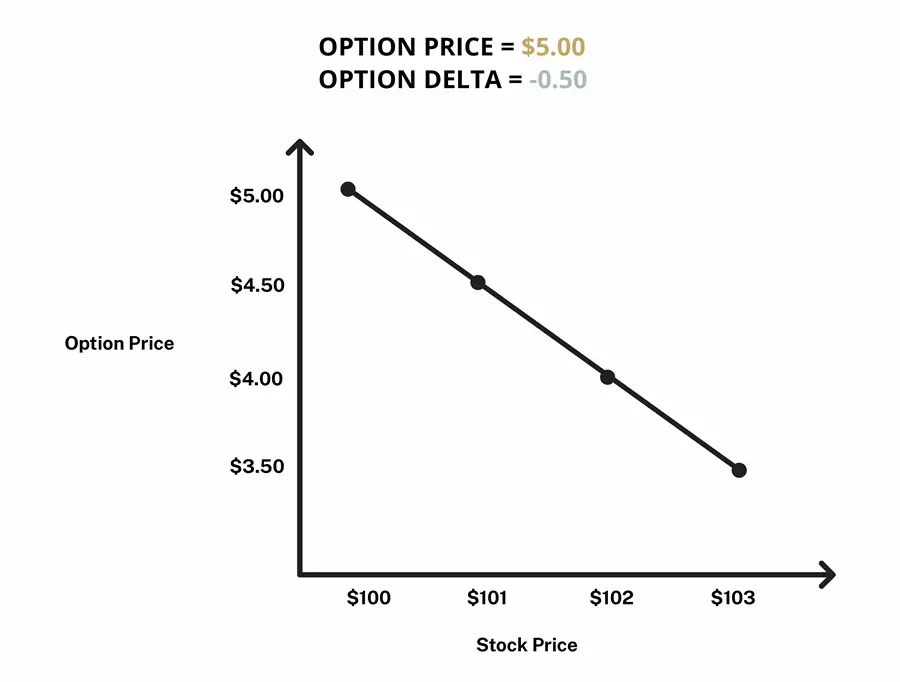
A delta value of -1 for put options means that the put option is deeply in-the-money and will move in lockstep with the underlying cryptocurrency’s price. A delta of -0.50 means that the put option is at-the-money and has a 50% chance of expiring in-the-money.
In-The-Money vs. Out-Of-The-Money Option Delta
Broadly speaking, delta values reflect if the option is “in the money” or “out of the money”. In-the-money options contracts exhibit a higher delta relative to out-of-the-money options, owing to their higher sensitivity to changes in the price of the underlying cryptocurrency.

For in-the-money options, delta is usually closer to 1 for call options and -1 for put options. This means that every dollar change in the price of the underlying cryptocurrency will result in a $1 change in the price of the option.
For out-of-the-money options, the delta generally approaches 0 for both call and put options. This means that alterations in the underlying cryptocurrency’s price have minimal impact on the option's value.
At-The-Money Call & Put Options
Call and put options that are at-the-money exhibit deltas near 0.50 and -0.50, respectively. It implies that the options carry a 50% probability of reaching maturity while in-the-money. The reason for this is that the strike prices of the at-the-money options are close to the current price of the underlying asset.
How Delta is Calculated
You can calculate option delta using option models, such as the Black-Scholes model. In this model, the delta of a call option is calculated as follows:
Δ = N(d1)
where N(d1) is the standard normal distribution for d1. The formula for d1 is as follows:
d1 = [ln(S/K) + (r + σ^2/2)t] / (σ√t)
where:
S - the current price of the underlying asset;
K - strike price of the option;
r - risk-free interest rate;
σ - standard deviation of the price of the underlying asset;
t - time to expiration of the option.
Similarly, the delta of a put option can be calculated as follows:
Δ = N(d1) - 1
where N(d1) is a standard normal distribution indicator for d1, and d1 is calculated the same way as for call options.
Uses of Delta
Delta for Short vs. Long Options Position
Depending on the direction of the option position, the delta can take different values. Essentially, there are two sides to the trade — the option seller and the option buyer. The seller opens short positions, while the buyer opens long positions.
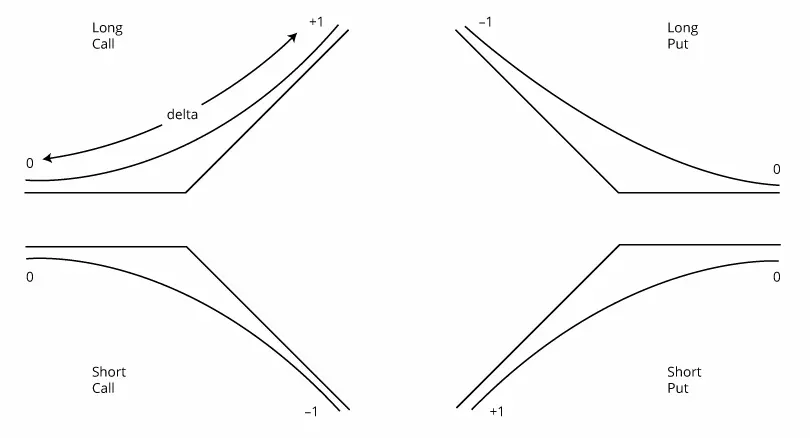
So far, we have discussed the delta parameters for long positions. For a long call option position, the delta has a range between 0 and 1. The more the option is in-the-money, the closer it is to 1. And the delta for long put options takes values from 0 to -1. Thus, the put option in-the-money will have a value of -1.
A short position reverses the delta. For example, a short call will have a negative delta between 0 and -1, and a short put will have a positive delta between 0 and 1. Thus, for the seller, the closer the short call option is to -1, the more in-the-money it is. And vice versa for short-put options.
Position
Investors opening multiple options positions should also take into account such estimates as position delta. Position delta is a measure of the total delta of all options in a portfolio. It is calculated as the sum of the deltas of all options in the portfolio multiplied by the number of options in each position:
Position Delta = ∑(Δ x n)
where Δ is the delta of each option in the portfolio and n is the number of options in each position. The amount is taken for all options in the portfolio.
For example, if the portfolio has 2 call options with a delta of 0.6 each and 3 put options with a delta of -0.4 each, then the position delta for that portfolio would be:
Position Delta = (2 x 0.6) + (3 x (-0.4)) = 1,2 - 1,2 = 0
This means that the total delta for this portfolio is zero, which may indicate neutrality with respect to changes in the value of the underlying asset. However, in reality, there may be other factors affecting the risk and profitability of a portfolio other than position delta.
Three Additional Uses of Delta
In addition to evaluating the risk and potential reward of options positions, delta can be used for three additional purposes.
Directional Bias
An investor's viewpoint about the price trajectory of the underlying cryptocurrency is referred to as directional bias. Delta can be employed to determine an investor's directional bias. For instance, the trader holds a call option with a delta of 0.80. In such a scenario, they will be bullish on the underlying crypto asset, as an increase in the asset's price would likely result in the option expiring in-the-money.
However, directional bias can be misleading and may not coincide with the actual price movement of the cryptocurrency. Investors should therefore consider other factors, such as volatility, end of life, no risk bet, and other Greeks when selecting strategies.
Hedge Ratio
Delta can also be utilized for determining the hedge ratio, which represents the ratio between the number of options and the required amount of the underlying cryptocurrency needed to establish a hedged position.
The hedge ratio can be defined as the ratio of the total delta of options positions to the price of the underlying instrument in the portfolio. For example, if a portfolio has a long position in 10 call options with a delta of 0.5 each and the value of the underlying cryptocurrency is $50 per share, the hedge ratio for that portfolio would be:
Hedge Ratio = (10 × 0.5) / 50 = 0.1
In our case, this means that to protect against potential risks in the portfolio, we need to sell 0.1 of the cryptocurrency for each call option in the portfolio.
Probability Indicator
Delta can be used as a probability indicator, indicating the likelihood of an option expiring in-the-money. For example, if a call option has a delta of 0.70, it has a 70% chance of expiring in-the-money.
It is worth noting that a delta value higher than 0.5 is not a guarantee that the option will expire in-the-money. Especially in the crypto market, there is a chance that the underlying cryptocurrency will suddenly move in the opposite direction.
Shifts in Delta Scores
Delta values can change based on changes in market conditions, such as changes in the price of the cryptocurrency, changes in the risk-free interest rate, or changes in volatility:
- An increase in the underlying cryptocurrency leads to the increase of call options delta and decrease in put options delta;
- Both call and put options deltas increase if volatility increases;
- Delta approaches 1 as the option nears expiration.
Conclusion
Delta serves as a valuable tool for options traders, which helps to understand the responsiveness of an option to changes in the value of the underlying digital asset. Grasping this Greek can empower traders to control risks and make well-informed decisions in their trading activities. Utilizing delta, traders can build a variety of trading strategies, including directional betting, hedging, and probability-based trades.
FAQ
What Is Delta in Options Trading?
Delta describes the sensitivity (rate of change) of an option’s price with respect to changes in the underlying price. Delta is a measure of an option's sensitivity to changes in the price of the underlying instrument. The options with high delta (close to 1 for calls, close to -1 for puts) are considered deep in-the-money (ITM).
How Is Delta Calculated?
Delta can be calculated using the following formula:
Delta = Change in Option Price / Change in Underlying Asset Price
The Black-Scholes model and the Binomial model are commonly used to calculate delta values for options contracts.
How Can Delta Be Used in Options Trading?
Delta can be used in a variety of ways to construct trading strategies and manage risk, including directional bets, hedges, and probability-based trades.
Can Delta Change Over Time?
Yes, delta values can shift based on changes in the underlying asset's price, volatility, and time to maturity. Traders should regularly monitor their positions and adjust them as needed based on changes in delta values.
*This communication is intended as strictly informational, and nothing herein constitutes an offer or a recommendation to buy, sell, or retain any specific product, security or investment, or to utilise or refrain from utilising any particular service. The use of the products and services referred to herein may be subject to certain limitations in specific jurisdictions. This communication does not constitute and shall under no circumstances be deemed to constitute investment advice. This communication is not intended to constitute a public offering of securities within the meaning of any applicable legislation.




